Answer: (1500.66,1599.34)
Explanation:
Confidence interval for population mean:

,where
 = Sample mean , n= Sample size, z* = critical two tailed z-value ,
= Sample mean , n= Sample size, z* = critical two tailed z-value ,
 = population standard deviation.
= population standard deviation.
As per given , we have
n= 16
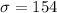 square feet
square feet
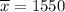 square feet
square feet
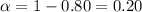
Critical z-value =
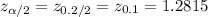
Confidence interval for population mean:

Required confidence interval: (1500.66,1599.34)