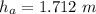Answer:
The value is
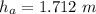
Step-by-step explanation:
From the question we are told that
The height of the top meter stick above the ground is
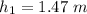
The time taken for the acorn to pass the length of the stick is
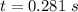
Generally the height of the acorn at the point it is the same height with the metered stick is mathematically represented as
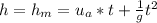
Here
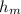 is height of the meter stick and the value is 1 m (This because we are told in the question that the stick is 1 meter in length ( a meter stick))
is height of the meter stick and the value is 1 m (This because we are told in the question that the stick is 1 meter in length ( a meter stick))
So
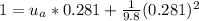
=>

Generally the velocity of the acorn just before passing the top of the meter stick is mathematically represented by a kinematic equation as
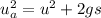
here u is zero since the acorn started from rest
So
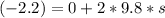
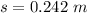
Generally the height of the acorn is
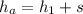
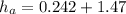 \
\