Answer:
The answer is below
Step-by-step explanation:
a) Since sales of the company increases at a constant rate, it means that the function is a linear function. Let the time in months be the independent variable x and the sales be the dependent variable y. It can be represented as (x, y)
At 2 months the company sells 12 products, this can be represented by (2, 12). Also after 8 months the company sells 30,000 products, this can be represented by (8, 30000). The formula for a linear function is:
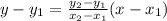
Using (2, 12) and (8, 30000):
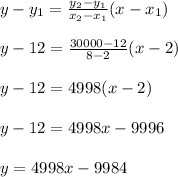
b) For a sales of 145000, i.e y = 145000
y = 4998x - 9984
145000 = 4998x - 9984
4998x = 145000 + 9984
4998x = 154984
x = 31.009
It would take about 31.009 months to make a sales of 145000