Question

(10 pts) (a) (2 pts) What is the difference between an ordinary differential equation and an initial value problem? (b) (2 pts) What is the difference between a particular solution and a general solution? (c) (3 pts) Given an example of a second-order linear ODE and a second-order nonlinear ODE that is not in the text, Chapter 1. (d) (3 pts) Give an example of a nonlinear 4th-order ordinary differential equation.

Answer 1

Explanation:

(A) The difference between an ordinary differential equation and an initial value problem is that an initial value problem is a differential equation which has condition(s) for optimization, such as a given value of the function at some point in the domain.

(B) The difference between a particular solution and a general solution to an equation is that a particular solution is any specific figure that can satisfy the equation while a general solution is a statement that comprises all particular solutions of the equation.

(C) Example of a second order linear ODE:

M(t)Y"(t) + N(t)Y'(t) + O(t)Y(t) = K(t)

The equation will be homogeneous if K(t)=0 and heterogeneous if
`K(t)\\eq 0`

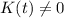
Example of a second order nonlinear ODE:

`Y=-3K(Y){2}`

(D) Example of a nonlinear fourth order ODE:

`K^4(x) - \beta f [x, k(x)] = 0`