Answer:
Vertex of g(x) is (4, -1)
Explanation:
Method 1
Using translations rules:
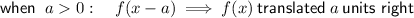
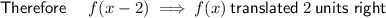
If the vertex of f(x) is (2, -1)
then the vertex of g(x) is (2 + 2, -1) = (4, -1)
Method 2
Vertex form of a parabola

(where (h, k) is the vertex and a is some constant)
Given function:
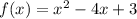
If the vertex of f(x) is (2, -1), then f(x) written in vertex form is:
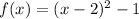

Therefore, the vertex of g(x) is (4, -1)