Question

a golf ball is launched straight up with an initial velocity of 15.68m/s. Calculate the balls displacement and velocity every 0.4 sec into the ball's flight. How long will it take the ball in the air?​

Answer 1

Step-by-step explanation:

Given:

v₀ = 15.68 m/s

a = -9.8 m/s²

t = 0.4n s, n = 0, 1, 2, etc.

Find: Δy and v

To find displacement, use the equation:

Δy = v₀ t + ½ at²

To find velocity, use the equation:

v = at + v₀

`\left\begin{array}{ccc}t&y&v\\0&0&15.68\\0.4&5.49&11.76\\0.8&9.41&7.84\\1.2&11.76&3.92\\1.6&12.54&0\\2.0&11.76&-3.92\\2.4&9.41&-7.84\\2.8&5.49&-11.76\\3.2&0&-15.68\end{array}\right`

The ball lands after 3.2 seconds.

Answer 2

calculated velocities:

(t,v(t))

(0.4,11.756)

(0.8,7.832)

(1.2,3.908)

(1.6,-0.016)

calculated displacements:

`(t,\Delta x)`

(0.4, 5.487)

(0.8,9.4048)

(1.2, 11.7528)

(1.6, 12.5312)

the ball spends 3.2 seconds in the air

Step-by-step explanation:

Assuming the ball is launched on earth with standard gravity and that the effects of drag is neglected.

assume that 'up' is positive direciton since that is direction of travel

'down' is negative direction

formula for velocity is
`v(t)=v_0+at`

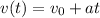
where
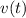`v(t)` is the velocity at time
`t`

`v_0` is the initial velocity at time
`t=0`

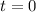
`a` is the acceleration in the direction of the velocity

velocity is in m/s and accelration is in m/s^2 and t is in seconds

for displacement:
`\Delta x=v_0 t+(1)/(2)at^2`

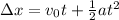
Known stuffs:

in our case, we know we are on earth so,
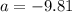`a=-9.81`m/s^2. the negative sign indicates that the direction is oposite the velocity since the ball travels up but gravity pulls down

the initial velocity is given as
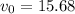`v_0=15.68`m/s

therefore, our equation for velocity is

`v(x)=15.68-9.81t`

now we just need to plot it every 0.4 seconds

this is easy subsituteion. here's the first:

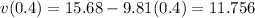`v(0.4)=15.68-9.81(0.4)=11.756`m/s

if we keep plotting this, we get the following table

(t,v(t))

(0.4,11.756)

(0.8,7.832)

(1.2,3.908)

(1.6,-0.016) the velocity is negative meaning that the ball is now going 'down' and therefor the ball has just passed the peak of it's upward travel

so since it took about 1.6 seconds to get here, it will spend about twice this time in the air or about 3.2 seconds

to get an exact answer, solve for the time when velocity is 0, ie when the ball has reached its peak and stopped moving

set
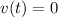`v(t)=0` and solve for t

`0=15.68-9.81t\rightarrow 15.68=9.81t\rightarrow t=1.598s`

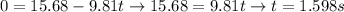
so it takes 1.598 seconds to get to peak, therefore it spends twice this time in the air or 3.197 seconds in the air. it's close enough to 3.2 seconds

the ball spends 3.2 seconds in the air

displacement:

`\Delta x=v_0t+(1)/(2)at^2`

`\Delta x=15.68t+(1)/(2)(-9.81)t^2`

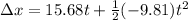
some values are

`(t,\Delta x)`

(0.4, 5.487)

(0.8,9.4048)

(1.2, 11.7528)

(1.6, 12.5312)