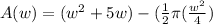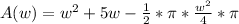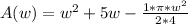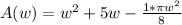Answer:

Explanation:
A = the area of the region outside the semicircle but inside the rectangle
w = the width of the rectangle or diameter of the semicircle
Since "A" is determined by "w", therefore, "A" is a function of "w" = A(w).
A(w) = (area of rectangle) - (area of semicircle)
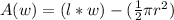
Where,
lenght of rectangle (l) = w + 5
width of rectangle (w) = w
r = ½*w =
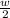
Plug in the values:
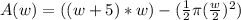
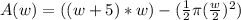
Simplify