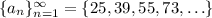We're given the sequence,
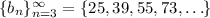
Since
 is quadratic,
is quadratic,
 should also be quadratic. Replace
should also be quadratic. Replace
 with
with
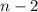 (if
(if
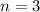 , then
, then
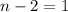 ) in the definition of
) in the definition of
 , and let
, and let
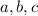 denote the new coefficients:
denote the new coefficients:
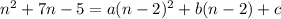
Expand the right side:
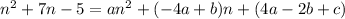
Coefficients of terms with the same degree should be the same:
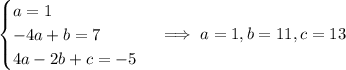
So the new sequence is the same, with