Answer:
(-2, 1) and (6, 1)
Explanation:
The standard form equations for a hyperbola are ...
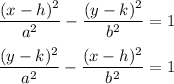
The first form opens horizontally; the second opens vertically. Further, the center-focus distance 'c' is given by ...
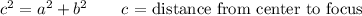
The attached figure illustrates the relation between the various parameters and the features of the hyperbola.
__
7.
Using the above information and the information in the first attachment, we find ...
(h, k) = (2, 1)
a = 4, b = 2
The vertices are (h±a, k), so are (2±4, 1) = (-2, 1) and (6, 1).
__
The second attachment illustrates the hyperbola and its vertices.