Determine the minimum and maximum angles to the nearest tenth of a degree that a pipe can make with the horizontal. the minimum angle being 1/4 inch the maximum angle being 1/2 …

Question

asked Jan 23, 2021 8.5k views

1 Answer

Tomomi · Answer 1 · 2021-01-30T19:30:47+0000

Given :

A pipe can make with the horizontal. the minimum angle being 1/4 inch the maximum angle being 1/2 inch .

To Find :

The minimum and maximum angles to the nearest tenth of a degree that a pipe can make with the horizontal.

Solution :

Angle
$\theta$ is given by :

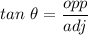
$tan\ \theta=(opp)/(adj)$

Now , minimum angle is given by :

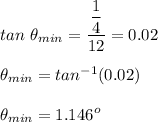
$tan\ \theta_(min)=((1)/(4))/(12)=0.02\\\\\theta_(min)=tan^(-1)(0.02)\\\\\theta_(min)=1.146^o$

For maximum angle :

$tan\ \theta_(max)=((1)/(2))/(12)=0.04\\\\\theta_(max)=tan^(-1)(0.04)\\\\\theta_(max)=2.291^o$

Therefore , minimum and maximum angle is 1.146° and 2.291° respectively .

Hence , this is the required solution .