Answer:
Approximately
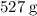 .
.
Step-by-step explanation:
Look up relative atomic mass data on a modern periodic table:
Calculate the formula mass of
 and
and
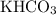 (the two reactants,) as well as
(the two reactants,) as well as
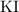 (the product.)
(the product.)
The question states that
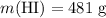 while
while
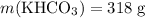 . Calculate the number of moles of formula units in each of these two reactants:
. Calculate the number of moles of formula units in each of these two reactants:
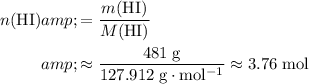 .
.
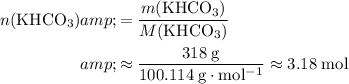 .
.
Note that in the balanced equation of this reaction, the ratio between the coefficients of
 ,
,
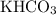 , and
, and
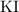 is
is
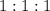 .
.
Therefore, for every mole of
 formula units consumed, one mole of
formula units consumed, one mole of
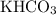 formula units will also be consumed, while one mole of
formula units will also be consumed, while one mole of
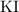 formula units will be produced.
formula units will be produced.
Similarly, for every mole of
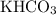 formula units consumed, one mole of
formula units consumed, one mole of
 formula units will also be consumed, while one mole of
formula units will also be consumed, while one mole of
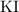 formula units will be produced.
formula units will be produced.
Assume that
 is in excess. If all these (approximately)
is in excess. If all these (approximately)
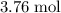 of
of
 formula units are consumed,
formula units are consumed,
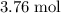 of
of
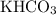 formula units will also need to be consumed. However, that's not possible because there was only approximately
formula units will also need to be consumed. However, that's not possible because there was only approximately
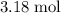 of
of
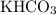 formula units available.
formula units available.
On the other hand, if
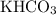 is in excess, all these (approximately)
is in excess, all these (approximately)
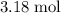 moles of
moles of
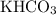 formula units would be consumed. At the same time, approximately
formula units would be consumed. At the same time, approximately
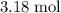 of
of
 would be consumed- which is indeed possible because approximately
would be consumed- which is indeed possible because approximately
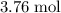 of
of
 formula units are available. Therefore, up to approximately
formula units are available. Therefore, up to approximately
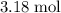 of
of
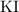 formula units will be produced.
formula units will be produced.
Calculate the mass of that
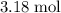 of
of
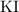 formula units:
formula units:
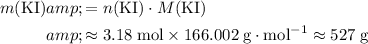 .
.