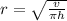Answer:
B.
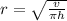
Explanation:
We are given the formula:
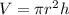
and asked to solve for
 . Therefore, we must isolate
. Therefore, we must isolate
 on one side of the equation.
on one side of the equation.
 and
and
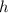 are both being multiplied by r². The inverse of multiplication is division. Divide both sides of the equation by
are both being multiplied by r². The inverse of multiplication is division. Divide both sides of the equation by
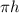 .
.
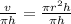
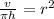
r is being squared. The inverse of a square is a square root. Take the square root of both sides of the equation.
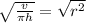
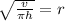
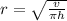
Therefore, the correct answer is B.