Answer:
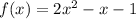
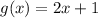
Explanation:
Let the two polynomials be represented with f(x) and g(x);
Since, we have to generate the polynomial ourselves;
I'll make use of the following:
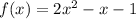
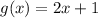
Note that; when the result of polynomial division is referred to as quotient;
To get the quotient, we simply divide f(x) by g(x)
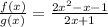
Expand the numerator
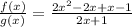
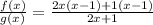
Factorize:
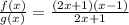
Cross out 2x + 1
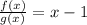
This implies that, the quotient, Q(x) is
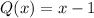
Comparing the divisor g(x) and the quotient Q(x), we notice that they have the same degree of 1