Question

Write two polynomial functions whose quotient will be the same degree as the divisor.

Answer 1

`f(x) = 2x^2 - x - 1`

`g(x) = 2x + 1`

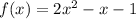
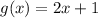
Explanation:

Let the two polynomials be represented with f(x) and g(x);

Since, we have to generate the polynomial ourselves;

I'll make use of the following:

`f(x) = 2x^2 - x - 1`

`g(x) = 2x + 1`

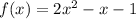
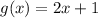
Note that; when the result of polynomial division is referred to as quotient;

To get the quotient, we simply divide f(x) by g(x)

`(f(x))/(g(x)) = (2x^2 - x - 1)/(2x + 1)`

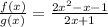
Expand the numerator

`(f(x))/(g(x)) = (2x^2 - 2x + x - 1)/(2x + 1)`

`(f(x))/(g(x)) = (2x(x - 1) +1(x - 1))/(2x + 1)`

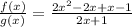
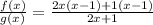
Factorize:

`(f(x))/(g(x)) = ((2x + 1)(x - 1))/(2x + 1)`

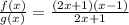
Cross out 2x + 1

`(f(x))/(g(x)) = x - 1`

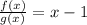
This implies that, the quotient, Q(x) is

`Q(x) = x - 1`

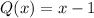
Comparing the divisor g(x) and the quotient Q(x), we notice that they have the same degree of 1