Answer :
Step by step Step-by-step explanation :
We know,
sin θ =
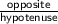
here,
sin 0 =
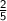
So,
opposite must be 2
and hypotenuse will be 5
Now,
By Pythagoras theorem
Adjacent =
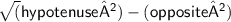
=> Adjacent =
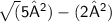
=> Adjacent =
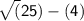
=> Adjacent =
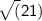
Now as adjacent =
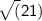
We know,
cos θ =

=> cos θ =
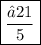
Hope this helps you!
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
The calculation is lengthy but if you know the concept then it's very easy
I would suggest you to learn all the trigonometric ratios and these trigonometric functions.
Thank you!