Answer:
V = (About) 22.2, Graph = First graph/Graph in the attachment
Explanation:
Remember that in all these cases, we have a specified method to use, the washer method, disk method, and the cylindrical shell method. Keep in mind that the washer and disk method are one in the same, but I feel that the disk method is better as it avoids splitting the integral into two, and rewriting the curves. Here we will go with the disk method.
![\mathrm{V\:=\:\pi \int _a^b\left(r\right)^2dy\:},\\\mathrm{V\:=\:\int _1^3\:\pi \left[\left(1+(2)/(y)\right)^2-1\right]dy}](https://img.qammunity.org/2021/formulas/mathematics/college/ansr2quibeoymk5k49bj37t8ugl0rqz7nr.png)
The plus 1 in '1 + 2/x' is shifting this graph up from where it is rotating, but the negative 1 is subtracting the area between the y-axis and the shaded region, so that when it's flipped around, it becomes a washer.
![V\:=\:\int _1^3\:\pi \left[\left(1+(2)/(y)\right)^2-1\right]dy,\\\\\mathrm{Take\:the\:constant\:out}:\quad \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx\\=\pi \cdot \int _1^3\left(1+(2)/(y)\right)^2-1dy\\\\\mathrm{Apply\:the\:Sum\:Rule}:\quad \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx\\= \pi \left(\int _1^3\left(1+(2)/(y)\right)^2dy-\int _1^31dy\right)\\\\](https://img.qammunity.org/2021/formulas/mathematics/college/jp4o3z6xqic56mnn22yhjqk8lp3yre7ecq.png)
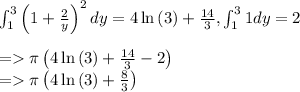
Our exact solution will be V = π(4In(3) + 8/3). In decimal form it will be about 22.2 however. Try both solution if you like, but it would be better to use 22.2. Your graph will just be a plot under the curve y = 2/x, the first graph.