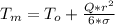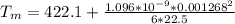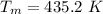Question

An electric current of 200 A is passed through a stainless steel wire having a radius R of 0.001268 m. The wire is L = 0.91 m long and has a resistance R of 0.126 Ohm. The outer surface temperature Tw is held at 422.1 K. The average thermal conductivity is K = 22.5 W/mK. Calculate the center temperature. Power = I^2R (Watts) Where I = current in nmps and R = Resistance in ohms I^2R (Watts) = q pi(Radius)^2L

Answer 1

The value is
`T_m  =  435.2 \  K`

Step-by-step explanation:

From the question we are told that

The current is
`I  =  200 \ A`

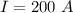
The radius is
`R =  0.001268 \  m`

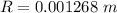
The length of the wire is
`L  =  0.91 \  m`\

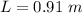The resistance is
`R  =  0.126 \  \Omega`

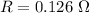
The outer surface temperature is
`T _o  =  422.1 \  K`

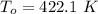
The average thermal conductivity is
`\sigma  =  22.5 W/mK`

Generally the heat generated in the stainless steel wire is mathematically represented as

`Q =  (Power)/( \pi r^2L)`

`Q =  (I^2 R)/( \pi r^2L)`

=>
`Q =  (200^2 * 0.126)/(3.142 *  (0.001268)^2 * 0.91)`

=>
`Q =  1.096*10^(9)\  W/m^3`

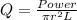
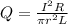
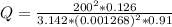
Generally the middle temperature is mathematically represented as

`T_m  =  T_o  + (Q * r^2 )/( 6  * \sigma )`

`T_m  =  422.1  +  (1.096*10^(-9) * 0.001268^2)/(6 * 22.5)`

`T_m  =  435.2 \  K`