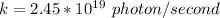Answer:
a
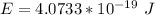
b
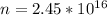
c
tex]k = 2.45 *10^{19} \ photon / second[/tex]
Step-by-step explanation:
From the question we are told that
The wavelength is
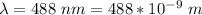
The power is
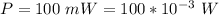
The diameter of the circle is
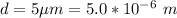
The time taken is
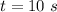
Generally the energy of the photon is mathematically represented as

substituting
 for h ,
for h ,
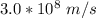 for c
for c
So
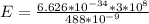
=>
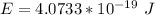
Generally the number of photons emitted is mathematically
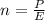
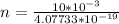
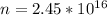
Generally the number of photons emitted in by the laser in ten seconds is mathematically
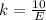
=>
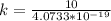
=>