Question

How do you do this question?

Answer 1

9π

Explanation:

Start by graphing the region. The region bound by y = x, x = 3, and y = 0 is a triangle. When rotated about the x-axis, the resulting shape is a cone.

First, let's find the volume using integration. To do that, slice the cone into circular disks. Each disk has a thickness of dx, and a radius of y. So the volume of each disk is:

dV = π r² h

dV = π y² dx

y = x, so:

dV = π x² dx

The total volume is the sum of all the disks from x=0 to x=3:

V = ∫ dV

V = ∫₀³ π x² dx

Integrating:

V = π/3 x³ |₀³

V = π/3 (3)³ − π/3 (0)³

V = 9π

We can check our answer using geometry. Volume of a cone is:

V = ⅓ π r² h

V = ⅓ π (3)² (3)

V = 9π

Answer 2

Solution : Option B, or 9π

Explanation:

We are given that y = x, x = 3, and y = 0.

Now assume we have a circle that models the given information. The radius will be x, so to determine the area of that circle we have πx². And knowing that x = 3 and y = 0, we have the following integral:

`\int _0^3`

So our set up for solving this problem, would be such:

`\int _0^3x^2\pi \:`

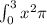
By solving this integral we receive our solution:

`\int _0^3x^2\pi dx,\\\mathrm{Take\:the\:constant\:out}:\quad \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx\\=> \pi \cdot \int _0^3x^2dx\\\mathrm{Apply\:the\:Power\:Rule}:\quad \int x^adx=(x^(a+1))/(a+1)\\=> \pi \left[(x^(2+1))/(2+1)\right]^3_0\\=> \pi \left[(x^3)/(3)\right]^3_0\\\mathrm{Compute\:the\:boundaries}: \left[(x^3)/(3)\right]^3_0=9\\\mathrm{Substitute:9\pi }`

As you can tell our solution is option b, 9π. Hope that helps!