Since points J, Q, and M are collinear of JM, and JQ, the values of x and y as an ordered pair is (9.5, 19.5).
In this scenario, line ratio would be used to determine the coordinates of the point M on the directed line segment JM and JQ that partitions the segment into a ratio of 2 to 3.
In Mathematics and EuclideanGeometry, line ratio can be used to determine the coordinates of a point and this is modeled by this mathematical equation:
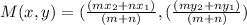
By substituting the given points J (2, 7) and Q (5, 12) into the formula for line ratio, we have;
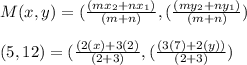
By solving the equation in part for the value of x and y, we have;

2x = 25 - 6
x = 19/2
x = 9.5
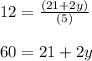
2y = 60 - 21
y = 39/2
y = 19.5
In conclusion, we can logically deduce that point M is located at (9.5, 19.5).
Complete Question:
Points J,Q, and M are collinear of JM, and JQ: QM=2/3.
J is located at (2,7), Q is located at (5,12), and M is located at (x, y).
What are the values of x and y?