Answer:
Explanation:
Equation of a parabola is represented by,
f(x) = -a(x - h)² + k [Parabola opening downwards]
where (h, k) is the vertex of the parabola.
Picture attached shows the vertex as (-1, -2)
Therefore, equation of the transformed parabola will be,
f(x) = -a(x + 1)²- 2
Since the given parabola passes through a point (1, -3)
-3 = -a(1 + 1)² - 2
-1 = -4a²
a =
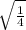
a =

Therefore, equation of the transformed function will be,
f(x) =
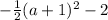
If the original or parent function is g(x) = x²,
Transformed function will have the following characteristics,
1). Function will have vertex as (-1, -2) opening downwards.
2). Graph passes through (-3, -3) and (1, -3).
3). Reflection across x-axis.
4). Translation of 2 units down and 1 unit to the left.
5). Horizontal stretch by a factor of 2.