Question

1. Let D(t) represent the amount of drug in a patient (measured in grams) at time t (measured in hour). The initial amount of drug is 90 grams. After 2 hours the amount is 70 grams. Assuming that the amount of drug decays erponentially, address the following

problems.

(a) Write down a differential equation that best describes the growth of the amount
of the drug.

(b) Find the general solution to the differential equation in part (a).

(c) Use the additional provided information to determine D(t).

(d) What is the half-life for D(t)?​

Answer 1

a. dD(t)/dt = -kD(t) b.
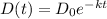`D(t) = D_(0)e^(-kt )` c.
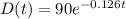`D(t) = 90e^(-0.126t )` d. 5.5 hours

Explanation:

a. The differential equation that models the growth of the dD(t)/dt is

-dD(t)/dt ∝ D(t)

dD(t)/dt = -kD(t)

b. The general solution of the equation in a. is gotten below

dD(t)/dt = -kD(t)

separating the variables, we have

dD(t)/D(t) = -kdt

Integrating both sides, we have

∫dD(t)/D(t) = -∫kdt

㏑D(t) = -kt + c

`D(t) = e^(-kt + c)\\ D(t) = e^(-kt )e^(c)\\D(t) = D_(0)e^(-kt ) (D_(0) = e^(c))`

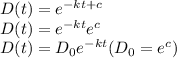
c. Given that when t = 2 hours, D(t) = 70 grams and D₀ = initial amount of drug = 90 grams

Substituting these values into the equation, we have

`D(t) = D_(0)e^(-kt ) \\70 = 90e^(-2k ) \\(70)/(90) = e^(-2k )\\\\`

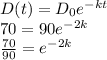
㏑(7/9) = -2k

k = -[㏑(7/9)]/2

= 0.2513/2

= 0.126

`D(t) = 90e^(-0.126t )`

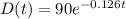
d. The half-life of the drug is the time when D(t) = D₀/2.

So

`D(t) = D_(0)e^(-0.126t )\\(D_(0))/(2) = D_(0)e^(-0.126t )\\(D_(0))/(2D_(0)) = e^(-0.126t )\\(1)/(2) = e^(-0.126t )`

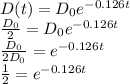
taking natural logarithm of both sides, we have

t = ㏑(1/2)/-0.126 = -0.693/-0.126 = 5.5 hours

So, the half-life is 5.5 hours