Answer:
C_{y} = 4.96 and θ' = 104,5º
Step-by-step explanation:
To add several vectors we can decompose each one of them, perform the sum on each axis, to find the components of the resultant and then find the module and direction.
Let's start by decomposing the two vectors.
Vector A
sin θ =
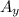 / A
/ A
cos θ = Aₓ / A
A_{y} = A sin θ
Ax = A cos θ
A_{y} = 4.9 sin 31 = 2.52
Ax = 4.9 cos 31 = 4.20
Vector B
B_{y} = B sin θ
Bx = B cos θ
B_{y} = 6 sin 156 = 2.44
Bx = 6 cos 156 = -5.48
The components of the resulting vector are
X axis
Cx = Ax + B x
Cx = 4.20 -5.48
Cx = -1.28
Axis y
C_{y} = Ay + By
C_{y} = 2.52 + 2.44
C_{y} = 4.96
Let's use the Pythagorean theorem to find modulo
C = √ (Cₙ²x2 + Cy2)
C = Ra (1.28 2 + 4.96 2)
C = 5.12
We use trigonemetry to find the angle
tan θ = C_{y} / Cₓ
θ’ = tan⁻¹ (4.96 / (1.28))
θ’ = 75.5
como el valor de Cy es positivo y Cx es negativo el angulo este en el segundo cuadrante, por lo cual el angulo medido respecto de eje x positivo es
θ’ = 180 – tes
θ‘= 180 – 75,5
θ' = 104,5º