Question

Find the range of values of m for which the roots of the equation below is real. 3x^2 - 3mx + (m^2 - m -3) = 0

Answer 1

The range is -2 ≤ m ≤ 6

Explanation:

Answer 2

In order for this polynomial (with respect to x) to have real roots, its discriminant should be non negative.

`9 {m}^(2) - (4 * 3 * ( {m}^(2) - m - 3) \geqslant 0`

Which means

`9 {m}^(2) - 12 {m}^(2) + 12m + 36 \geqslant 0`

`- 3 {m}^(2) + 12m + 36 \geqslant 0`

`{m}^(2) - 4m - 12 \leqslant 0`

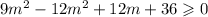
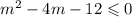
The last inequality is also a polynomial inequality.

The polynomial (with respect to m) has the following discriminant:

`{4}^(2) - 4 * - 1 * 12 * 1 = 16 + 48 = 64`

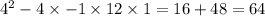
Thus the roots of this polynomial are:

`(4( + - )8)/(2) = 6 \: and \: - 1`

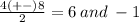
When a polynomial has two positive roots named y, z for example where y<z the sign of the polynomial goes as following.

If the coefficient of the highest order term is positive then the polynomial is positive for m<y and m>z and negative for y<m<z.

If the coefficient of the highest order term is negative then the polynomial is negative for m<y and m>z and positive for y<m<z.

In the polynomial:

`{m}^(2) - 4m - 12`

The coefficient of the highest order term is 1 thus the polynomial is non positive at the interval [-1,6].

Thus the solution to the exercise is

`- 1 \leqslant m \leqslant 6`

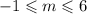
I apologize for any typos or wrong calculations.