Question

Please someone help me to prove this. ​

Answer 1

Hope this can help.

Answer 2

Answer: see proof below

Explanation:

Use the following Sum Identity:

`\tan (A + B) =(\tan A+\tan B)/(1-\tan A\cdot \tan B)`

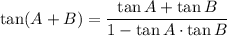
Given: A + B + C = 180° → A + B + C = π

Proof LHS → RHS

Given: A + B + C = π

Multiply by 2: 2(A + B + C = π)

→ 2A + 2B + 2C = 2π

→ 2A + 2B = 2π - 2C

Apply tan: tan(2A + 2B = 2π - 2C)

→ tan (2A + 2B) = tan(2π - 2C)

→ tan (2A + 2B) = - tan 2C

`\text{Sum Identity:}\qquad \qquad (\tan 2A+\tan 2B)/(1-\tan 2A\cdot \tan 2B)=-\tan 2C`

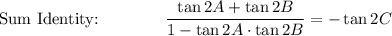
Simplify: tan 2A + tan 2B = -tan 2C (1 - tan 2A · tan 2B)

Distribute: tan 2A + tan 2B = -tan 2C + tan 2A · tan 2B · tan 2C

Add tan 2C: tan 2A + tan 2B + tan 2C = tan 2A · tan 2B · tan 2C

LHS = RHS is proven