Answer:
The fire hydrant = 9 meters west and south of the tower = 58 m
Explanation:
The coordinate as the origin includes the Fire A and Fire B
Given that
Fire A is 75 meters east and south of the tower is 40 meters
So, it is presented (75,-40)
And, the fire B is 37 west and south of the tower is 64 meters
So, it is presented (-37,-64)
Now at a point O (x,y) divides AB a line segment as A(x_1, y_1) and B(x_2, y_2)
So,
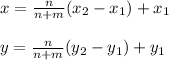
Now it divides in three-fourth
So,


Hence, these two are to be considered