Question

You are given a 16-bit binary integer X= (1110 0100 0111 1010)2 . Convert X to decimal if:

a. X is unsigned
b. X is in sign-magnitude notation
c. X is in one’s complement notation
d. X is in two’s complement notation

Answer 1

The binary integer X can be converted to decimal differently based on the given notation: as an unsigned integer it is 58426, in sign-magnitude notation it is -22650, in one's complement notation, it is -22651, and in two's complement notation, it is -22650.

Step-by-step explanation:

To convert the 16-bit binary integer X = (1110 0100 0111 1010)2 to decimal, we must treat it differently based on the specified notation.

When X is unsigned, all bits contribute to the value. Starting from the right (least significant bit), each bit represents a power of 2, corresponding to its position. Calculating the sum of these values:

1*(2^15) + 1*(2^14) + 1*(2^13) + 0*(2^12) + ... + 1*(2^1) + 0*(2^0) = 58426.

In sign-magnitude notation, the leftmost bit is the sign bit (1 for negative, 0 for positive), and the remaining bits represent the magnitude. Since the sign bit is 1, the value is negative, thus:

-((0*(2^14) + 1*(2^13) + 1*(2^12) + ... + 1*(2^1) + 0*(2^0))) = -22650.

In one's complement notation, a negative number is represented by inverting all bits of its positive counterpart. If the leftmost bit (sign bit) is 1, the value is negative. Flip all bits and add 1 to determine the magnitude:

-(1*(2^14) + 0*(2^13) + 0*(2^12) + ... + 0*(2^1) + 1*(2^0)) = -22651.

For two's complement notation, a negative number is the one's complement of its positive version, plus one. The calculation is similar to the one's complement: -(1*(2^14) + 0*(2^13) + 0*(2^12) + ... + 0*(2^1) + 1*(2^0) + 1) = -22650.

Answer 2

Step-by-step explanation:

a). The decimal numbers is equal to the sum of binary numbers
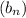`$(b_n)$` times their powers of
`$ 2(2^n) .$`

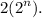
That is,

`$ b_n * 2^n + b_(n-1) 2^(n-1)+ ..... + b_02^0 $`

`$\therefore (1110 \ \ 0100 \ \ 0111 \ \ 1010)_2 $`

=
`$ (0 * 2^0) + (1 * 2^1) + (0 * 2^2) + (1 * 2^3) + (1 * 2^4) + (1 * 2^5) + (1 * 2^6) + ( 0 * 2^7) + (0 * 2^8) + (0 * 2^9) + (1 * 2^(10) ) $`
`$ + (0 * 2^(11)) + (0 * 2^(12)) + (1 * 2^(13)) + (1 * 2^(14))+ (1 * 2^(15))$`

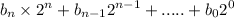
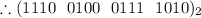
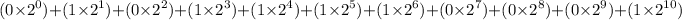
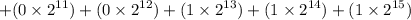
= 58490

b).

The left most bit of the number represents the sign of the number. If bit = 1, the number is negative else if the bit is 0, the number is positive.

All the remaining bits (i.e all the bits except the leftmost bit) represent the magnitude of the number.

Now, X = 1110 0100 0111 1010

left most bit = 1 => number is negative

remaining bits Y = 110 0100 0111 1010

converting Y to decimal => Y = 25722

c).

Check the leftmost bit(lmb) of the number

if leftmost bit is 0 => convert do the binary to decimal conversion

if leftmost bit is 1, follow the following steps

1. Flip the bits (convert the 0's into 1's and the vice versa)

2. convert the new number from binary to decimal.

3. Add a negative sign / multiply by -1

Now, X = 1110 0100 0111 1010

left most bit = 1;

flipping the bits => Y = 0001 1011 1000 0101

converting Y into decimal => Y = 7045

multiplying Y with -1 => Y = -7045

Therefore, one's complement of X to decimal is -7045

Thus, X = -25722 in decimal.

d).

Check the leftmost bit(lmb) of the number

if leftmost bit is 0 => convert do the binary to decimal conversion

if leftmost bit is 1, follow the following steps

1. Flip the bits (convert the 0's into 1's and the vice versa)

2. convert the new number from binary to decimal.

3. Add 1 to the converted number

4. Add a negative sign / multiply by -1

Now, X = 1110 0100 0111 1010

left most bit = 1;

flipping the bits => Y = 0001 1011 1000 0101

converting Y into decimal => Y = 7045

Adding 1 to Y => Y = 7046

multiplying Y with -1 => Y = -7046

Thus, two's complement of X to decimal is -7046