Answer:
Width is 19.24 ft and length is 24.24 ft
Explanation:
Step 1: Write an equation
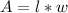
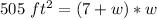
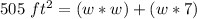

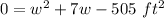
Step 2: Determine the dimensions
Use Quadratic formula

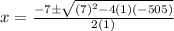
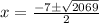

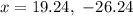
Since length cannot be negative, we will use 19.24 for x.
Step 3: Determine the length
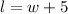
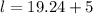
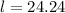
Answer: Width is 19.24 ft and length is 24.24 ft