Complete question:
The acceleration of a particle traveling along a straight line is a = 1/4 s^1/2 m/s^2, where s is in meters. If v = 0, s = 1 m when t = 0, determine the particle’s velocity at s = 2 m.
Answer:
The particle’s velocity is 0.781 m/s.
Step-by-step explanation:
Given;
acceleration of the particle,
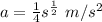
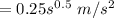
Acceleration is given by;
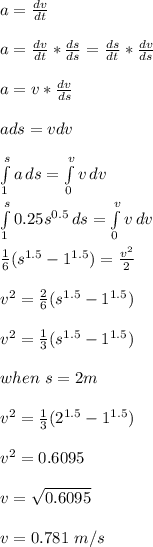
Therefore, the particle’s velocity at s = 2 m, is 0.781 m/s.