Answer:
slope of the tangent
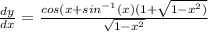
The function y = f(x)
y(x) = 2 x + C
Explanation:
Step(i):-
Given x= sin t ...(i)
Differentiating equation (i) with respective to 'x' , we get
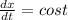
Given y = sin ( t + sin (t)) ...(ii)
Differentiating equation (ii) with respective to 'x' , we get
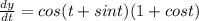
Step(ii):-
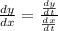
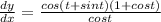
we know that
x = sin t
t = sin⁻¹ (x)
cost = √1 - sin²(t) = (√1-x²)
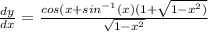
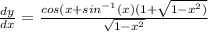
Put x =0 and y=0
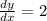
d y = 2 d x
Integrating with respective to 'x' , we get
y(x) = 2 x + C