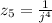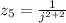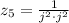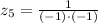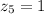Answer:
a.
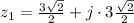 , b.
, b.
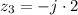 , c.
, c.
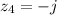 , d.
, d.
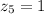
Explanation:
All given complex numbers are in polar form, which are characterized by:

Where:
 - Magnitude, dimensionless.
- Magnitude, dimensionless.
 - Direction, measured in radians.
- Direction, measured in radians.
The rectangular form of complex numbers is represented by:
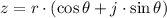
Now, each complex number is evaluated:
a.
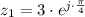
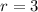 and
and
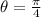
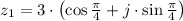
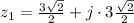
b.
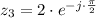
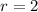 and
and
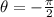
![z_(3) = 2\cdot \left[\cos \left(-(\pi)/(2)\right) + j\cdot \sin \left(-(\pi)/(2) \right) \right]](https://img.qammunity.org/2021/formulas/mathematics/college/8kdfkf05dsxkm0kz704uxsovrnoxpxm7fa.png)
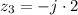
c.
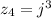
By definition of complex number,
 , which means that
, which means that
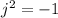 . Hence:
. Hence:
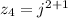
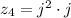
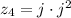
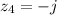
d.
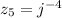
By definition of complex number,
 , which means that
, which means that
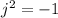 .
.
Hence: