Answer:
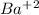 = 0.3 M
= 0.3 M
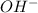 = 0.6 M
= 0.6 M
Step-by-step explanation:
We can start wit the ioniation reaction:
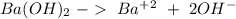
We have the ions
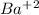 and
and
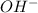 . Now, we can calculate the concentration of each ion:
. Now, we can calculate the concentration of each ion:
Concentration of
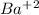
In balanced reaction we have 1 mol of
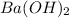 and 1 mol of
and 1 mol of
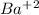 , so, we have a 1:1 mol ratio, with this in mind:
, so, we have a 1:1 mol ratio, with this in mind:

Concentration of
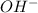
In balanced reaction we have 1 mol of
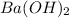 and 2 mol of
and 2 mol of
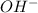 , so, we have a 1:2 mol ratio, with this in mind:
, so, we have a 1:2 mol ratio, with this in mind:
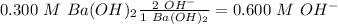
I hope it helps!