Answer:
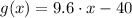 ; The team shall earn $ 632 for selling 70 candles.
; The team shall earn $ 632 for selling 70 candles.
Explanation:
We notice that statement indicate that every worker gains 80 percent of the revenue for selling candles, which is represented
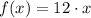 , where
, where
 is the quantity of sold candles and
is the quantity of sold candles and
 is measured in US dollars, minus 40 US dollars. Then, the mathematical expression
is measured in US dollars, minus 40 US dollars. Then, the mathematical expression
 is formed by three components:
is formed by three components:
1) Revenue for selling candles:

2) 80 % of the revenue for selling candles: Vertical scaling (
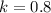 )
)
3) $ 40 are subtracted: Vertical translation. (
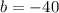 )
)
Then, the expression for
 is:
is:
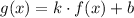
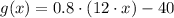
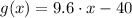
Where:
 - Quantity of candles, dimensionless.
- Quantity of candles, dimensionless.
 - Team's profit, measured in US dollars.
- Team's profit, measured in US dollars.
Finally, we determine the profit for selling 70 candles: (
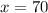 )
)
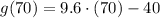
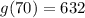
The team shall earn $ 632 for selling 70 candles.