Answer: The width is
 + 1x -4
+ 1x -4
Explanation:
We know to find the perimeter we have to add the distance around the rectangle.The distance can also be sought as 2 times the length plus times the width.
So as a formula is like P = 2l + 2w where P is the perimeter.
We are given the perimeter so we can plot it into the formula and also plot in the length because it says the length is 3x -1
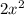 +8x - 10 = 2(3x -1) + 2w Now we have to solve for w .Break it down
+8x - 10 = 2(3x -1) + 2w Now we have to solve for w .Break it down
(
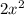 + 8x -10) = (6x -2 )+ 2w subtract 6x - 2 from both sides
+ 8x -10) = (6x -2 )+ 2w subtract 6x - 2 from both sides
(
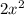 + 8x -10) - (6x -2) = 2w
+ 8x -10) - (6x -2) = 2w
(
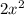 + 2x -8) = 2w now divide both sides by 2
+ 2x -8) = 2w now divide both sides by 2
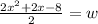 One the left side factor the numerator
One the left side factor the numerator
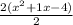 = w Now multiply both sides by 2
= w Now multiply both sides by 2
w =(
 + 1x-4 )
+ 1x-4 )
The width is x^2 + 1x -4