Question

A rectangle has a perimeter of 2x^2+8x-10 the length of the rectangle is 3x-1. What is the width as an expression

Answer 1

Answer: The width is
`x^(2)` + 1x -4

Explanation:

We know to find the perimeter we have to add the distance around the rectangle.The distance can also be sought as 2 times the length plus times the width.

So as a formula is like P = 2l + 2w where P is the perimeter.

We are given the perimeter so we can plot it into the formula and also plot in the length because it says the length is 3x -1

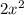`2x^(2)`+8x - 10 = 2(3x -1) + 2w Now we have to solve for w .Break it down

(
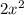`2x^(2)` + 8x -10) = (6x -2 )+ 2w subtract 6x - 2 from both sides

(
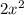`2x^(2)` + 8x -10) - (6x -2) = 2w

(
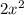`2x^(2)` + 2x -8) = 2w now divide both sides by 2

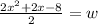`(2x^(2) +2x-8 )/(2) = w` One the left side factor the numerator

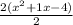`(2(x^(2) +1x-4))/(2)` = w Now multiply both sides by 2

w =(
`x^(2)` + 1x-4 )

The width is x^2 + 1x -4