Question

Noah’s Café sells special blends of coffee mixtures. Noah wants to create a 20-pound mixture with coffee that sells for $9.20 per pound and coffee that sells for $5.50 per pound. How many pounds of each mixture should he blend to create coffee that sells for $6.98 per pound? a 10 pounds of the $5.50-per-pound coffee, 10 pounds of the $9.29-per-pound coffee b 15 pounds of the $5.50-per-pound coffee, 5 pounds of the $9.20-per-pound coffee c 12 pounds of the $5.50-per-pound coffee, 8 pounds of the $9.20-per-pound coffee d 8 pounds of the $5.50-per-pound coffee, 12 pounds of the $9.29-per-pound coffee

Answer 1

Answer: c 12 pounds of the $5.50-per-pound coffee, 8 pounds of the $9.20-per-pound coffee

Explanation:

Let x = Number of pound of first king.

y= Number of pound of second kind.

As per given , we have

`x+y=20\Rightarrow\ y= 20-x (i)\\\\\\9.20x +5.50 y= 6.98(20) \\\Rightarrow\ 9.20x +5.50 y=139.6 (ii)`

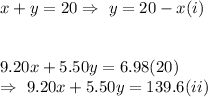
substitute value of y from (i) in (ii), we get

`9.20x +5.50(20-x) =139.6\\\\\Rightarrow\ 9.20x +5.50(20)-5.50x =139.6\\\\\Rightarrow\ 9.20x-5.50x +110 =139.6\\\\\Rightarrow\ 3.7x =139.6-110\\\\\Rightarrow\ 3.7x =29.6\\\\\Rightarrow\ x=(29.6)/(3.7)=(296)/(37)\\\\\Rightarrow\ x=8`

Put this in (i), we get y= 20-8 = 12

Hence, he should blend 12 pounds of the $5.50-per-pound coffee, 8 pounds of the $9.20-per-pound coffee.

So the correct option is c.