Question

Given the vector equation ????(t)=(4−3t)????+(−5+t)????+(3−t)????, rewrite this in terms of the parametric equations for the line.x(t)=

y(t)=
z(t)=

Answer 1

The parametric equations for the line.x(t)=

y(t)=

z(t)=

is

`\= r (t) =  \left \{ {{x(t)= 4-3t} \atop {y(t)= -5+t}}  \atop {z(t)=3-t}} \right \}`

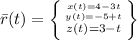
Explanation:

From the question we are told that

the given equation is

`\= r(t) =  (4-3t) + (-5 + t) + (3-t)`

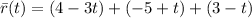
This given equation can be represented as

`\= r (t) =  [4 -3t , -5+t,3-t]`

Generally this equation can be represented in terms of the parametric equations as follows

`\= r (t) =  \left \{ {{x(t)= 4-3t} \atop {y(t)= -5+t}}  \atop {z(t)=3-t}} \right \}`

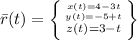
This above equation is obtained by assigning each component of r(t) to each line