Question

an object of mass 8 kg is wild around rapidly in a vertical circle of radius 2 metres with constant speed of 6 m per second calculate the maximum tension in the string​

Answer 1

`\boxed{\sf Maximum \ tension \ (T_(max)) = 224 \ N}`

Given:

Mass (m) = 8 kg

Constant speed (v) = 6 m/s

Radius of vertical circle (r) = 2 m

Accelration due gravity (g) = 10 m/s²

To Find:

Maximum tension in the string (
`\sf T_(max)`)

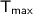Step-by-step explanation:

As the object is moving in a vertical circular path. So, the maximum tension on the string is when the body will be on its lowest position because at that point centrifugal force and force due to gravity both will act on the body in same direction.

So,

Maximum tension (
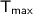`\sf T_(max)`) is the string will be equal to centrifugal force (
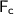`\sf F_c`) + Force due to gravity.

`\boxed{ \bold{ T_(max) = F_c + mg= \frac{m {v}^(2) }{r} + mg }}`

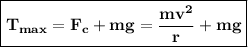
Substituting value of m, v, r & g in the equation:

`\sf \implies T_(max) = \frac{8 * {6}^(2) }{2} + 8 * 10 \\ \\ \sf \implies T_(max) = (8 * 36)/(2) + 80 \\ \\ \sf \implies T_(max) = (8 * 36)/(2) + 80 \\ \\ \sf \implies T_(max) = (288)/(2) + 80 \\ \\ \sf \implies T_(max) = 144 + 80 \\ \\ \sf \implies T_(max) = 224 \: N`

`\therefore`

Maximum tension in the string (T) = 224 N