
- The angle between the two vectors is 90° .

- The dot product of two vectors .
- The cross product of two vectors .

⚡ Let
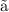 and
and
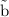 are the two vectors .
are the two vectors .
✍️ We have know that,
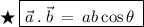
Where,
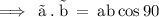
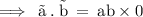
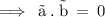
 [1] The dot product of two vectors is “ 0 ” .
[1] The dot product of two vectors is “ 0 ” .
✍️ We have know that,
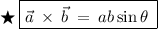
Where,
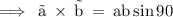
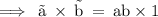
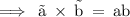
 [2] The cross product of two vectors is “ ab ” .
[2] The cross product of two vectors is “ ab ” .