Question

If h(x) = -2x+5/4, find h(x) = 3/4

Answer 1

x = 1/4

Explanation:

We are given the function as h(x) = - 2x + 5/4. If we have to determine h(x) = 3/4 given this function, let's substitute this value into our function and solve for 'x.' This will be our solution -

3/4 = - 2x + 5/4,

If we subtract 5/4 from either side : - 2x = - 1/2

Now divide either side by - 2 : x = 1/4

Therefore our solution is x = 1/4

Answer 2

`x=(1)/(4)`

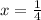
Explanation:

So we have the function:

`h(x)=-2x+(5)/(4)`

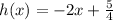
And we want to find h(x)=3/4.

So, we want to find the value of x such that h(x) equates to 3/4.

So, substitute 3/4 for h(x):

`(3)/(4)=-2x+(5)/(4)`

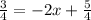
First, subtract both sides by 5/4. The right will cancel.

`(3)/(4)-(5)/(4)=-2x+(5)/(4)-(5)/(4)`

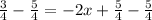
Subtract on the left:

`-(2)/(4)=-2x`

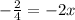
Reduce on the left:

`-(1)/(2)=-2x`

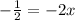
Now, multiply both sides by -1/2. The right will again cancel:

`-(1)/(2)(-(1)/(2))=-(1)/(2)(-2x)`

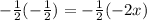
Multiply on the left:

`x=(1)/(4)`

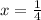
So, for h(x) to be 3/4, the value of x is 1/4.

And we're done!