Answer:
The restaurant is not at half way
Explanation:
Given
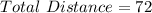
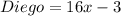
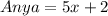
Required
Accept or reject Diego's claim
To do that, we need to determine the value of x by:
Diego + Anya =Total Distance
Substitute values for each parameter
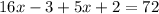
Collect Like Terms
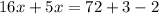
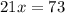
Divide both sides by 21
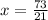
Substitute the value of x in Diego and Anya's distance
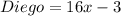
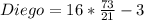
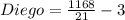
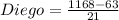
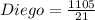

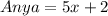
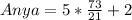
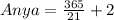
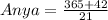
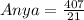
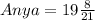
Since, both distances are not equal,
Then Diego's claim is false and incorrect