Answer:
A quadratic equation can be written as:
a*x^2 + b*x + c = 0.
where a, b and c are real numbers.
The solutions of this equation can be found by the equation:
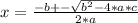
Where the determinant is D = b^2 - 4*a*c.
Now, if D>0
we have the square root of a positive number, which will be equal to a real number.
√D = R
then the solutions are:
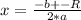
Where each sign of R is a different solution for the equation.
If D< 0, we have the square root of a negative number, then we have a complex component:
√D = i*R
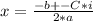
We have two complex solutions.
If D = 0
√0 = 0
then:
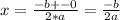
We have only one real solution (or two equal solutions, depending on how you see it)