Answer: β ≠ ±1
Explanation: For a system of equations to have an unique solution, its determinant must be different from 0: det |A| ≠ 0. So,
det
![\left[\begin{array}{ccc}1&\beta&1-\beta\\2&2&0\\2-2\beta&4&0\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/c4uo9pzs1s8fz1k44yy05j8vu95r80ozep.png) ≠ 0
≠ 0
Determinant of a 3x3 matrix is calculated by:
det
![\left[\begin{array}{ccc}1&\beta&1-\beta\\2&2&0\\2-2\beta&4&0\end{array}\right]\left[\begin{array}{ccc}1&\beta\\2&2\\2-2\beta&4\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/41uyfxj4nhwvsr2ymbq2cdu2pjzxtodgwc.png)
![8(1-\beta)-[2(2-2\beta)(1-\beta)]](https://img.qammunity.org/2021/formulas/mathematics/college/az8359pfyi8oktah65uxmd0l6uoxtmlubr.png)
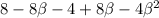
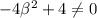
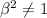
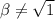
β ≠ ±1
For the system to have only one solution, β ≠ 1 or β ≠ -1.