Question

For which values of the parameter B the following system admits a unique solution [ 1 b 1-b 2 2 0 2–2B 4 0] [x y z] = [1 2 0]

Answer 1

Answer: β ≠ ±1

Explanation: For a system of equations to have an unique solution, its determinant must be different from 0: det |A| ≠ 0. So,

det
`\left[\begin{array}{ccc}1&\beta&1-\beta\\2&2&0\\2-2\beta&4&0\end{array}\right]` ≠ 0

Determinant of a 3x3 matrix is calculated by:

det
`\left[\begin{array}{ccc}1&\beta&1-\beta\\2&2&0\\2-2\beta&4&0\end{array}\right]\left[\begin{array}{ccc}1&\beta\\2&2\\2-2\beta&4\end{array}\right]`

`8(1-\beta)-[2(2-2\beta)(1-\beta)]`

`8-8\beta-4+8\beta-4\beta^(2)`

`-4\beta^(2)+4\\eq 0`

`\beta^(2)\\eq 1`

`\beta \\eq √(1)`

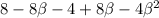
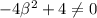
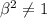
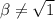
β ≠ ±1

For the system to have only one solution, β ≠ 1 or β ≠ -1.