Question

find the area of the trapezium whose parallel sides are 25 cm and 13 cm The Other sides of a Trapezium are 15 cm and 15 CM​

Answer 1

`\huge\underline{\red{A}\blue{n}\pink{s}\purple{w}\orange{e}\green{r} -}`

• Given - A trapezium ABCD with non parallel sides of measure 15 cm each ! along , the parallel sides are of measure 13 cm and 25 cm

• To find - Area of trapezium

Refer the figure attached ~

In the given figure ,

AB = 25 cm

BC = AD = 15 cm

CD = 13 cm

Construction -

`draw \: CE \: \parallel \: AD \: \\ and \: CD \: \perp \: AE`

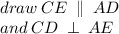
Now , we can clearly see that AECD is a parallelogram !

`\therefore` AE = CD = 13 cm

Now ,

`AB = AE + BE \\\implies \: BE =AB - AE \\ \implies \: BE = 25 - 13 \\ \implies \: BE = 12 \: cm`

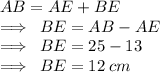
Now , In ∆ BCE ,

`semi \: perimeter \: (s) = (15 + 15 + 12)/(2) \\ \\ \implies \: s = (42)/(2) = 21 \: cm`

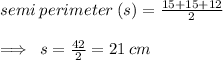
Now , by Heron's formula

`area \: of \: \triangle \: BCE = √(s(s - a)(s - b)(s - c)) \\ \implies √(21(21 - 15)(21 - 15)(21 - 12)) \\ \implies \: 21 * 6 * 6 * 9 \\ \implies \: 12 √(21) \: cm {}^(2)`

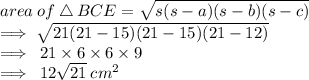
Also ,

`area \: of \: \triangle \: = (1)/(2) * base * height \\ \\\implies 18 √(21) = \: (1)/(\cancel2) * \cancel12 * height \\ \\ \implies \: 18 √(21) = 6 * height \\ \\ \implies \: height = \frac{\cancel{18} √(21) }{ \cancel 6} \\ \\ \implies \: height = 3 √(21) \: cm {}^(2)`

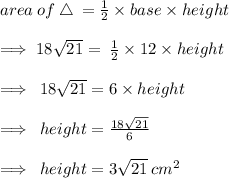
Since we've obtained the height now , we can easily find out the area of trapezium !

`Area \: of \: trapezium = (1)/(2) *(sum \: of \:parallel \: sides) * height \\ \\ \implies \: (1)/(2) * (25 + 13) * 3 √(21) \\ \\ \implies \: (1)/(\cancel2) * \cancel{38 }* 3 √(21) \\ \\ \implies \: 19 * 3 √(21) \: cm {}^(2) \\ \\ \implies \: 57 √(21) \: cm {}^(2)`

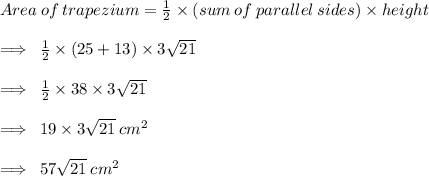
hope helpful :D