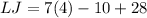Question

9. If LK MK, LK = 7x - 10, KN = x + 3, MN = 9x - 11, and KJ = 28, find LJ.

Answer 1

`LJ = 46`

Explanation:

Given:

`LK = MK`

`LK = 7x - 10`

`KN = x + 3`

`MN = 9x - 11`

`KJ = 28`

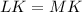
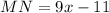
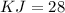
Required:

LJ

Solution:

Step 1: create an equation to find the value of x

Since we are given that LK = MK, and LK = 7x - 10, let's find the expression for MK to get an equation.

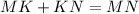`MK + KN = MN` (segment addition postulate)

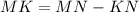`MK = MN - KN` (Subtract KN from each side)

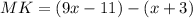`MK = (9x - 11) - (x + 3)` (subtitution)

`MK = 9x - 11 - x - 3`

`MK = 9x - x - 11 - 3`

`MK = 8x - 14`

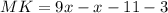
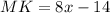
LK = MK, therefore,

`7x - 10 = 8x - 14`

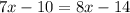
Subtract 8x from each side

`7x - 10 - 8x = 8x - 14 - 8x`

`-x - 10 = -14`

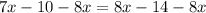
Add 10 to both sides of the equation

`-x - 10 + 10 = -14 + 10`

`-x = -4`

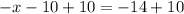
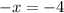
Divide both sides by -1

`x = 4`

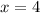
Step 2: Find LJ

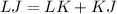`LJ = LK + KJ` (segment addition postulate)

`LJ = (7x - 10) + (28)`

Plug in the value of x

`LJ = 7(4) - 10 + 28`

`LJ = 28 - 10 + 28`

`LJ = 46`