The cross-sectional areas of a right pyramid and a right cylinder are congruent. The pyramid has a height of five units, and a right triangle has a height of three units. Which …

Question

asked Oct 20, 2021 56.4k views

1 Answer

NESHOM · Answer 1 · 2021-10-25T14:18:01+0000

Answer:

the volume of the right cylinder is 1.8 times the volume of the pyramid

Explanation:

The volume of a pyramid is

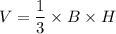
V = (1)/(3) * B* H

where the height of the pyramid is 5

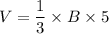
V = (1)/(3) * B* 5

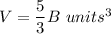
$V = (5)/(3) B \ units ^3$

On the other hand, the volume of a right cylinder is

V = BH

where the height of the right cylinder = 3 units

V = 3 B units³

Since we know that the cross-sectional areas are congruent, comparing the two-volume, we have the ratio of their volumes to be:

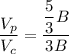
(V_p)/(V_c)= ((5)/(3)B)/(3B)

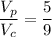
(V_p)/(V_c)= (5)/(9)

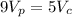
9 V_p = 5 V_c

$V_c = 1.8 \ V_p$

Hence, the volume of the right cylinder is 1.8 times the volume of the pyramid