Question

The Stokes-Oseen formula for drag force F on a sphere of diameter D in a fluid stream of low velocity V, density p and viscosity μ is

F=3πμDV+9π/16∗pV2d2
Is this formula dimensionally homogenous?

Answer 1

`(ML)/(T^2)=(ML)/(T^2)`

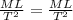
Hence it is proved that Stokes-Oseen formula is dimensionally homogenous.

Step-by-step explanation:

For equation to be dimensionally homogeneous both side of the equation must have same dimensions.

For given Equation:

F= Force, μ= viscosity, D = Diameter, V = velocity, ρ= Density

Dimensions:

`F=(ML)/(T^2)`

`\mu=(M)/(LT)`

`D=L\\\\V=(L)/(T)\\ \\\rho=(M)/(L^3)`

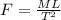
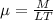
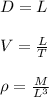
Constants= 1

Now According to equation:

`(ML)/(T^2)=[(M)/(LT)][L] [(L)/(T)] + [(M)/(L^3)][(L^2)/(T^2)][L^2]`

Simplifying above equation, we will get:

`(ML)/(T^2)=2*(ML)/(T^2)`

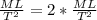
Ignore "2" as it is constant with no dimensions. Now:

`(ML)/(T^2)=(ML)/(T^2)`

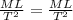
Hence it is proved that Stokes-Oseen formula is dimensionally homogenous.