Answer:
The volume of the solid = 1444
Step-by-step explanation:
Given that:
The region of the solid is bounded by the curves
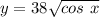 and the axis on
and the axis on
![[-(\pi)/(2), (\pi)/(2)]](https://img.qammunity.org/2021/formulas/mathematics/college/xk51pzqt0wzzv5xq0ahsp83p39w0sv3u5j.png)
using the slicing method
Let say the solid object extends from a to b and the cross-section of the solid perpendicular to the x-axis has an area expressed by function A.
Then, the volume of the solid is ;
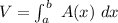
However, each perpendicular slice is an isosceles leg on the xy-plane and vertical leg above the x-axis
Then, the area of the perpendicular slice at a point
![x \ \epsilon \ [-(\pi)/(2),(\pi)/(2)]](https://img.qammunity.org/2021/formulas/mathematics/college/yjrnifv9jf40vule6fvns38r4ea2spj18i.png) is:
is:
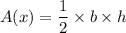
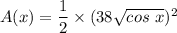
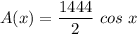
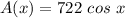
Applying the general slicing method ;
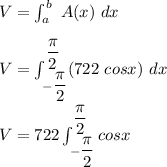
![V = 722 [ sin \ x ] ^{(\pi)/(2)}_{-(\pi)/(2)}](https://img.qammunity.org/2021/formulas/mathematics/college/k8k757hcipmwtpt0c496m8pdma61bye09z.png)
![V = 722 [sin (\pi)/(2) - sin (-(\pi)/(2))]](https://img.qammunity.org/2021/formulas/mathematics/college/ti86p73w4i4x0em6uwvjg17qdnvmieu1s4.png)
![V = 722 [sin (\pi)/(2) + sin (\pi)/(2))]](https://img.qammunity.org/2021/formulas/mathematics/college/8er7o9s2v5ht87vbhbvl2woz5gcf8crvsa.png)
![V = 722 [1+1]](https://img.qammunity.org/2021/formulas/mathematics/college/a1ebl1pluos84eeocoz13brav7hddfq71o.png)
![V = 722 [2]](https://img.qammunity.org/2021/formulas/mathematics/college/7h75v6a3lejrrrgar3c86figcomz2hsk2w.png)
V = 1444
∴ The volume of the solid = 1444