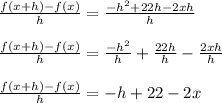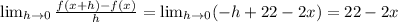Question

Find and simplify the following for ​f(x)=x(22-x), assuming h ≠ 0 in (C),a. f(x + h)b. f(x+h)- f(x)c. f(x+ h)- f(x)/h

Answer 1

The answer is below

Explanation:

Given that f(x)=x(22-x)

a) f(x)=x(22-x)

f(x + h) = (x + h)(22 - (x + h))

f(x + h) = (x + h)(22 - x - h)

f(x + h) = (22x - x² - xh + 22h - xh - h²)

f(x + h) = (-x² + 22x - h²+ 22h - 2xh)

b) f(x)=x(22-x) = 22x - x²

f(x + h) = (-x² + 22x - h²+ 22h - 2xh)

f(x+h)- f(x) = (-x² + 22x - h²+ 22h - 2xh) - (22x - x²)

f(x+h)- f(x) = -x² + 22x - h²+ 22h - 2xh - 22x + x²

f(x+h)- f(x) = -x² + x² + 22x - 22x - h²+ 22h - 2xh

f(x+h)- f(x) = - h²+ 22h - 2xh

c) f(x+h)- f(x) = - h²+ 22h - 2xh

`(f(x+h)-f(x))/(h)=(- h^2+ 22h - 2xh)/(h)\\ \\(f(x+h)-f(x))/(h)=(- h^2)/(h)+(22h)/(h)-(2xh)/(h)\\\\(f(x+h)-f(x))/(h)=-h+22-2x`

`\lim_(h \to 0) (f(x+h)-f(x))/(h)= \lim_(h \to 0) (-h+22-2x )=22-2x`